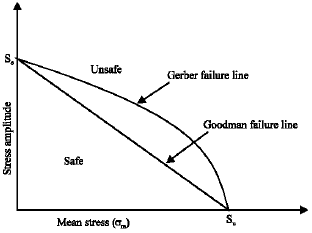
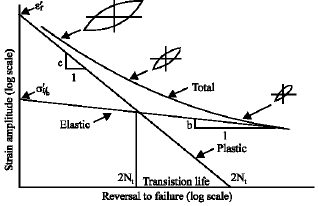
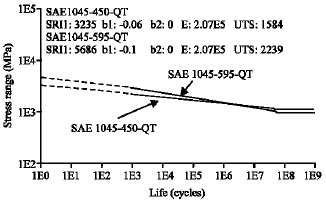
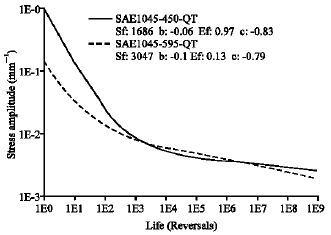
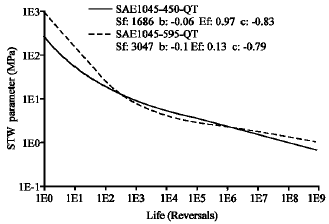
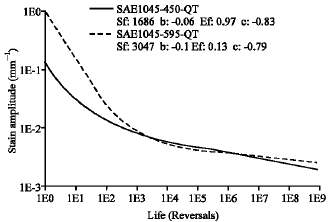
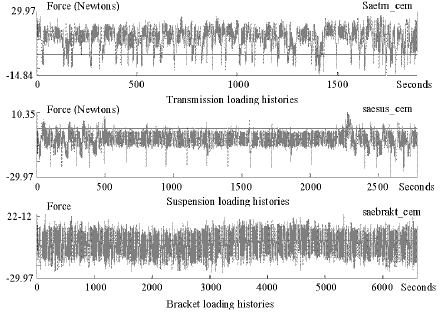
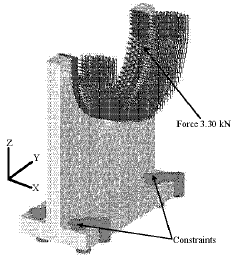
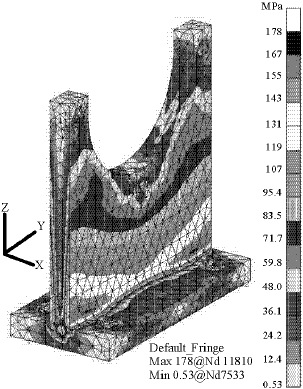
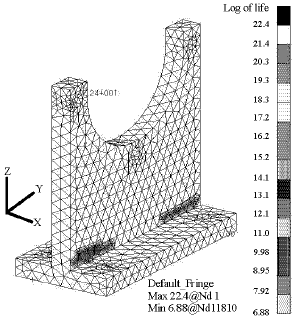
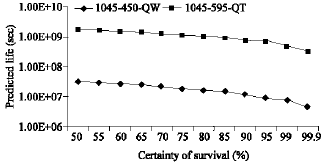
Research Article
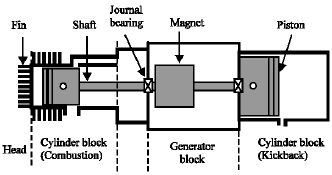
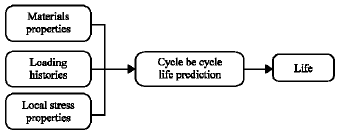
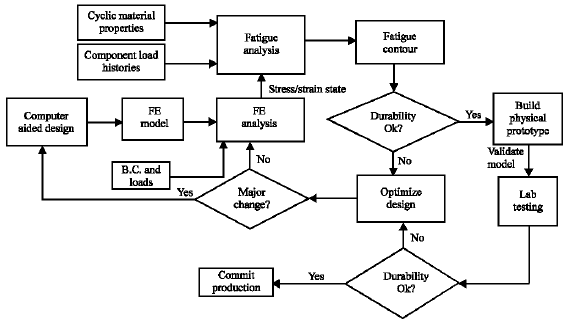
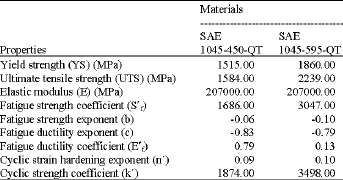
Finite Element Based Fatigue Life Prediction of a New Free Piston Engine Mounting
Automotive Excellence Center, Faculty of Mechanical Engineering, Universiti Malaysia Pahang, Locked Bag 12, 25000 Kuantan, Pahang, Malaysia
A.K. Ariffin
Department of Mechanical and Materials Engineering, Faculty of Engineering, Universiti Kebangsaan Malaysia, 43600 UKM, Bangi, Selangor, Malaysia
N. Jamaludin
Department of Mechanical and Materials Engineering, Faculty of Engineering, Universiti Kebangsaan Malaysia, 43600 UKM, Bangi, Selangor, Malaysia
S. Abdullah
Department of Mechanical and Materials Engineering, Faculty of Engineering, Universiti Kebangsaan Malaysia, 43600 UKM, Bangi, Selangor, Malaysia
M.M. Noor
Department of Mechanical and Materials Engineering, Faculty of Engineering, Universiti Kebangsaan Malaysia, 43600 UKM, Bangi, Selangor, Malaysia