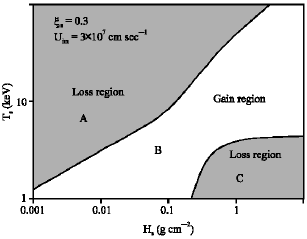
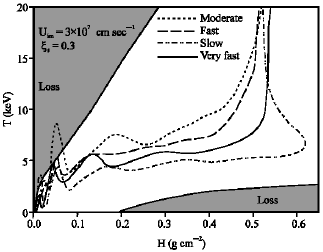
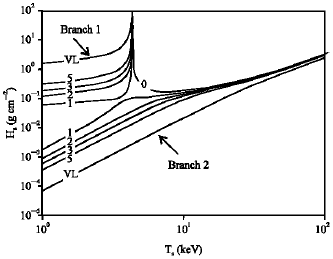
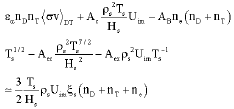Research Article
Ignition Criteria of Spark Parameters in Direct Drive Inertial Confinement Fusion
Department of Physics, University of Guilan, Rasht,P.O. Box 41335-1914, Guilan, Iran
Soheil Khoshbinfar
Department of Physics, University of Guilan, Rasht,P.O. Box 41335-1914, Guilan, Iran