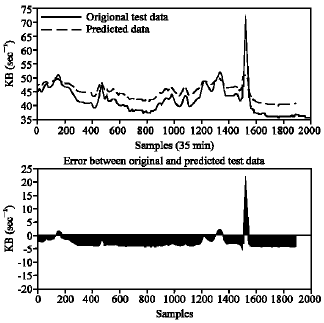
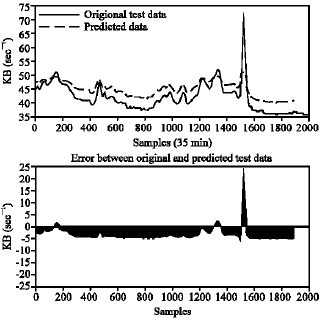
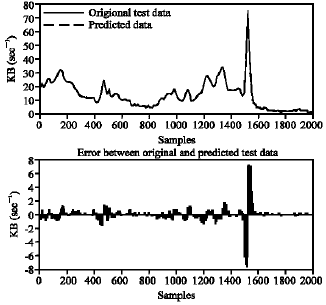
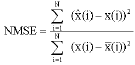Research Article
Short-Term Prediction of Traffic Rate Interval Router Using Hybrid Training of Dynamic Synapse Neural Network Structure
Department of Electrical Engineering, KN Toosi University of Technology, Tehran, Iran
M. Teshnehlab
Department of Electrical Engineering, KN Toosi University of Technology, Tehran, Iran
S. Zokaie
Department of Electrical Engineering, KN Toosi University of Technology, Tehran, Iran
M. Zakermoshfegh
Department of Civil Engineering, Jundi-Shapur University of Technology, Dezful, Iran