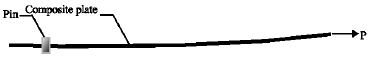Research Article
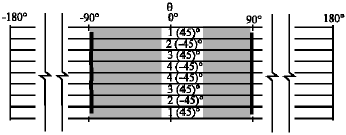
Three-Dimensional Solutions for Contact Area in Laminated Composite Pinned Joints with Symmetric and Non-Symmetric Stacking Sequences
Air Naval Research Center, Shiraz, Iran
I. Rajabi
Air Naval Research Center, Shiraz, Iran
V. Yavari
Department of Mechanical Engineering, Shiraz University, Shiraz, Iran
M. H. Kadivar
Department of Mechanical Engineering, Shiraz University, Shiraz, Iran