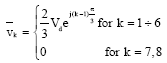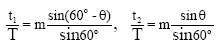Research Article
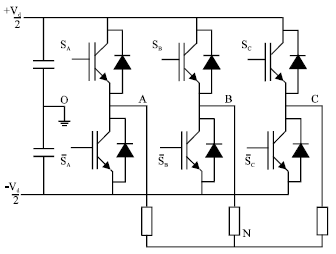
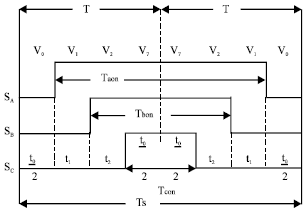
Modeling and Simulation of DSP Controlled SV PWM Three Phase VSI
Department of Machines and Electrical Drives, Faculty of Engineering, Annaba University, BP 12, El Hadjar 23000, Annaba, Algeria
A. Yousfi
Not Available
Y. Amirat
Not Available