ABSTRACT
In this research we study some types of limited sets and operators on non-archimedean locally convex spaces. We generate the concept of limited spaces into λ-limited spaces and study the relation between λ-limited spaces and λ-semiMontel spaces. We show that the non-archimedean locally convex space E is λ-limited space if and only if E is a space of type (Sλ).
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2007.978.983
URL: https://scialert.net/abstract/?doi=jas.2007.978.983
INTRODUCTION
In this research we study locally convex spaces over a complete valued scalar field K that are not isomorphic to R or C.We treat some theorems about compact sets and operators in functional analysis over R or C and discussion whether or not they remain valid in non-archimedean functional analysis. We study some types of limited sets and operators which called λ-limited sets and operators in non- archimedean locally convex spaces and we use the Kolmogrove diameters to obtain results resembling previously known properties of limited sets. We generate the concept of limited spaces into λ-limited spaces and study the relation between λ-limited spaces and λ-semi-Montel spaces.
PRELIMINARIES
Let K be a field. A non-Archimedean valuation on K is a function |.|:K→[0,∞) such that for all α,βεK it satisfies: |α| = 0 if and only if α = 0; |αβ| = |α||β| and |α+β|≤max{|α|,|β|}. Note that the last condition separates the absolute value on R or C from all other valuations. The mapping (λ,μ)→|λ-μ| is a metric on K making K into a topological field. We will call the valuation is dense if the set |K|\{0}, where |K| = {|λ|:λεK}, is dense in (0,∞).
Let E be a vector space over the field K. A non-archimedean seminorm on E is a seminorm which verifies the strong triangle inequality: ||a+b||≤max{||a,b||} for all a,bεE. If in addition ||x|| = 0⇔x = 0, then we say that ||.|| is a non-archimedean norm on E. The pair (E, ||.||) is called a non-archimedean normed space.
Throughout this study K will stand for a complete non- archimedean valued field, whose valuation is non-trivial. The collection of all continuous non-archimedean seminorm on a vector space E over K will be denoted by cs (E). For pεcs (E) and r>0, Bp (0, r) will be the set {xεE: p (x)≤r}. L (E, F) will be the vector space of all continuous linear operators from E into F. The non-archimedean normed space E is said to be of countable type if, there exists a countable subset S of E, such that the subspace [S] spanned by S is dense in E.
For a continuous non-archimedean seminorms p on E we put Ep = E/ker p and denoted by πp the canonical surjection πp: E→Ep. Then Ep is a non-archimedean normed space for the non-archimedean norm || ||p defined by ||πp(x)||p = p (x), xεE. By De Grande-De Kimpe and Perez-Garcia (1994) is a space of countable type.
The following sequence spaces will be need:
| • | |
| • | |
| • | |
| • | |
| • | |
| • |
Definition 1: A non-Archimedean sequence ideal λ on the valued field K is a subset of the space ι∞ (K) satisfying the following conditions:
| • | eiελ where ei = (0,0,...,1,....) the one in the ith place. |
| • | If x1, x2ελ, then x1+x2ελ. |
| • | If yει∞ (K) and xελ, then x.y ε λ. |
| • | If the sequence x = (x0,x1,.....)ελ, then (x0,x0, x1,x1,...)ελ. |
Note that the sequence spaces, ι∞ (K), c0 (K), (S), (R) and Λ (α) are examples of sequence ideals (Pietch, 1980).
For a bounded subset B of a locally convex space E over K, a pεcs (E) and a non-negative integer n, the nth Kolmogrove diameter δn,p(B) (or δn(B, Bp (0,1))) of B with respect to p is the infimum of all |μ|, μεK, for which there exists a subspace F of E with dim (F)≤n, such that A⊂F+μBp (0,1) (Katasars and Perez-Garcia, 1997). These nth Kolmogrove diameters satisfy the following properties:
Proposition 1:
| • | δ0,p(B)≥δ1,p(B)≥δ2,q(B)≥......≥0. for all pεcs (E). |
| • | If B1⊆B and p≤q, then δn,p(B1)≤δn,q (B). |
| • | If TεL (E, F), then for all pεcs(F) there exists qεcs (E) such that δn,p (T(B))≤δn,q (B). |
| • | If p′≥p, then δn (πp (Bq(0,1)), πp(Bp′(0,1))) = δn (Bq (0,1), Bp (0,1)) (Dubinsky, 1979; Jarchow, 1981; Safi, 2006). |
λ-LIMITED SETS
Definition 2: Let E, F be locally convex spaces over K, then
| • | A subset B of E is called compactoid if for every zero-neighborhood U in E there exists a finite set A⊂E such that B⊂co (A)+U, where co (A) is the absolutely convex hull of A. |
An operator TεL (E, F) is called compactoid if there exists a zero-neighborhood U in E such that T (U) is compactoid in F (De Grande-De Kimpe et al., 1995). Katasars and C. Perez-Garcia (1997) used the Kolmogrove diameters to give the following equivalent definition:
| • | The bounded subset B of a locally convex space E over K is called compactoid if and only if (Sn,p |
| • | A bounded subset B of E is called limited in E if and only if for each continuous linear map T from E to c0 (k), T (B) is compactoid in co (K). |
An operator TεL (E, F) is called limited if there exists a zero-neighborhood E in U such that T (U) is limited in F. We will denote by lim (E, F) the vector space of all limited operators from E to F ((De Grande-De Kimpe et al., 1995).
Parallel to this definitions we define the following:
Definition 3: Let E, F be locally convex spaces over K, then
| • | A subset B of E is called λ-compactoid if we replace co (K) in (1) |
| • | by the sequence ideal. |
An operator TεL (E, F) is called λ-compactoid if there exists a zero-neighborhood U in E such that T (U) is λ-compactoid in F. We will denoted by λ-C (E,F) the space of all λ-compactoid operators from E into F.
| • | A bounded subset B of E is called λ-limited in E if and only if for each continuous linear map T from E to co (K), T (B) is λ-compactoid in co (K). |
An operator TεL(E,F) is called λ-limited if there exists a zero-neighborhood U in E such that T (U) is λ-limited in F. We will denoted by (λ)-lim (E, F) the space of all λ-limited operators from E into F.
Notes:
| • | If dim (E) = n, then every bounded subset of E is λ-compactoid. |
| • | If |
| |
are two subsets of ι1 (K), then according to Pietch (1972) we have
| |
and
| |
where Bι1 is the closed unit ball in ι1. Hence D is c0 (K)- compactoid and (S)-compactoid, but not (R)-compactoid and B is c0 (K)-compactoid but not (S)-compactoid.
Proposition 2: Let E,F be locally convex spaces over K, then
| i) | Every λ-compactoid subset of E is λ-limited in E. |
| ii) | If B is λ-limited in E and TεL (E, F), then T (B) is λ-limited in F. |
| iii) | If B is λ-limited in E and D⊂B, then D is λ-limited in E. |
| iv) | If A is λ-limited, then |
| v) | If A, B⊂E are λ-limited in E, then A+B is λ-limited in E. |
| vi) | The product of any finite number of λ-limited sets is λ-limited. |
| vii) | Let M be a subspace of E and B⊂M. If B is λ-limited in M, then B is λ-limited in E (De-Grande-De Kimpe et al., 1995). |
Proof:
| • | Let B be any λ-compactoid subset of E and let TεL (E, c0(K)). It follows from property (iii) of proposition (1) that for all pεcs(F) there exists qεcs (E) such that δn, p (T (B))≤δn.q(B) and so T (B) is λ-compactoid in c0 (K). Therefore B is λ-limited in E. |
| • | Suppose B is λ-limited in E and TεL (E, F). Let GεL (F,c0 (K)), then GoTεL (E, c0(K)). It follows that G (T(B)) is λ-compactoid in c0(K) and so T(B) is λ-limited in E. |
| • | Let D⊂B and let TεL (E, F). Since T(D)⊂T (B), then by property (ii), (iii) of proposition (1) it follows that δn, p (T(D))≤δn, p for all pεcs (F). Since B is λ-limited in E, then T (D) is λ-compactoid in c0 (K) and this complete the proof. |
| • | From definition of δn,p (A), if ε>0 there exist a subspace F of E with dim(F)≤n and μεK such that |μ|≤δn,p(A)+ε, A⊆μBp(0,1)+F. It follows thatĀ⊆μBp (0,1)+F and so δn,p (A)≤|μ|≤δn,p(A)+ε. Since ε>0 is an arbitrary, we deduce that δn,p (Ā)≤ δn,p (A). That is, if A is λ-compactoid in E, then 0(K)). Since A is λ-limited it follows that T(A) is λ-compactoid and hence |
| • | Let TεL (E,c0) Since A, B are λ-limited, then T(A), T(B) are λ-compactoid. Since, T(A+B)⊆T(A)+T(B), it follows by Safi (2006) that T (A+B) is λ-compactoid in c0(K) and so A+B is λ-limited in E. |
| • | Let Di be any λ-limited set in Ei, i = 1,2,......, n and let E = E1xE2x.....xEn, TεL(E, c0(K)). Now If πi: Ei→E is conical inclusion, then the operator Ti = T○πiεL(Ei,co(K)) and so Ti (Di) is λ-compactoid in c0(K). Since, |
| |
then
| |
is λ-compactiod (Safi, 2006). Therefore
is λ-limited (proposition 2.i).
| • | Let M be a subspace of E and let B be λ-limited M. If TεL (E, F), then the restriction operator T|MεL (M, c0(K)). Since T|MεL(M,co(K)) is λ-compactoid in c0 (K) it follows that B is λ-limited in E. |
Note: If λ = c0 (K), then the unit ball ι∞ of is λ-limited, but not λ-compactoid (De Grande-Dekimpe and Perez-Garcia, 1994).
Definition 4: A locally convex space over K is called λ-Gelfand-Philips space (λ-GP-space in short) if every λ-limited set in E is λ-compactoid. (De Grande-Dekimpe and Perez-Garcia, 1994).
Remark : c0 (K) is λ-Gp space, for any sequence ideal λ (and hence any non-archimedean normed space of countable type (Van Rooij, 1978).
To see that let A be any λ-limited set in c0 (K). Since the identity operator IεL (c0(K), c0(K)), then I(A) = A is λ-compactoid.
λ-LIMITED SPACES
De Ggrande-de Kimpe and Perez-Garia (1994) give the following definition:
The locally convex space E over K is called limited space if L (E, F) = lim (E, F) for all non-archimedean normed space F.
Definition 5: We say that the locally convex space E over K is λ-limited space if L (E, F) = λ-lim (E,F) for all non-archimedean normed spaces F.
Notes:
| • | If λ = c0(K), then the concepts of λ-limited space coincide with the limited spaces and if the valuation K is dense. Then ι∞(K) is λ-limited spaces. Since L(c0 (K), c0 (K))≠λ-C(c0 (K), c0 (K))⊆λ-lim (c0 (K), c0 (K)), then c0 (K) is not λ-limited spaces (De Grande-De Kimpe et al., 1995). |
| • | If E is a non-archimedean normed space, then the closed unit ball of E, BE is λ-limited if L (E, c0 (K)) = λ-C (E, c0 (K)). |
Theorem 1: If L (E, F) = λ-lim (E, F) for any locally convex spaces E, F over K and M is a closed subspace of E then. L (E/M, F) = λ-lim (E/M, F).
Proof: Let M be a closed subspace of E and TεL (E/M, F). If π: E→E/M is the quotient map, then T○πεL (E, F). Since L (E, F) = λ-lim (E, F), there exists a zero-neighbourhood U in E such that (T○π(U) = T (π(U)) is λ-limited. Since π (U) is a zero-neighbourhood in E/M, then Tελ-lim (E/M, F).
Proposition 3: Let F, E1, E2, ..... be any locally convex spaces over K:
| • | If L (Ei, F) = λ-lim (Ei, F) for each iεN, then. |
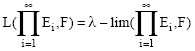 |
| • | If L (F, Ei) = λ-lim (F, Ei) for each iεI, I is finite, then |
| • | If Ei is λ-GP-space and L (F, Ei) = λ-lim (F, Ei) for each iεN, then |
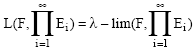 |
(Van Rooij, 1978).
Proof:
| • | Let |
 |
and let Tε(E, F). Then T is bounded on some zero-neighborhood W of E. This neighborhood can be taken in the form
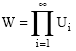 |
where Ui is a zero-neighborhood in Ei and the set J = {iεN: Ui≠Ei} is finite. So we can assume that E = E1xE2x.....xEn for some nεN. Now for i = 1, 2, ...., n, let πi: Ei→E be the conical inclusion. Since the operator Ti = T○πiεL (Ei, F) and L (Ei, F) = λ-lim (Ei, F), then there exists a zero- neighborhood Vi in Ei such that Ti (Vi) is λ-limited set in F, then V = VxV2x.....xVn is zero-neighborhood in E for which T(V) = T1(V1)+T2(V2)+.....+Tn (Vn) is λ-limited set in F (proposition (2.v)). So. Tελ-lim (E, F).
| • | Let |
I, is finite, and let Pi: E→Ei be the canonical operator, then Pi○TεL (F, Ei). Since L (F, Ei) = λ-lim (F,Ei), then Pi○T is λ-limited operator. Thus, there exists a zero-neighborhood U in F such that Pi○T (U) = Wi is λ-limited set in Ei. It follows by proposition (2.vi)
is λ-limited set in
and so T is λ-limited operator.
| • | Let |
 |
then like in part (ii) we can find a zero-neighborhood U in F such that Pi○T (U) = Wi is λ-limited set in Ei for all iεN. Since Ei is λ-GP-space, then Wi is λ-compactiod set in Ei. Now by Safi (2006)
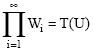 |
is λ-compactod set and by proposition (2.i) T(U) is λ-limited set in
Therefore
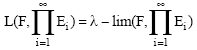 |
Definition 6: A locally convex space E over K is said to be of type (Sλ) if for each Pεcs(E) there exists qεcs(E) such that
for each q′≥p) (Zahriuita, 1973).
Proposition 4: The space E is of type (Sλ) if and only if E is λ-limited space.
Proof: Sufficiency, let E be λ-limited space and let pεcs(E). Since Ep = E/Ker p is a non-archimedean normed space and the canonical surjection
is continuous, then πp is λ- limited operator, so there exists a neighborhood Bq (0, 1) in E such that πp (Bq (0, 1) is λ-limited in Ep. Now since Ep is a non-archimedean normed space of countable type, then Ep is λ-Gp-space and so πp (Bq (0, 1) is λ-compactoid set in Ep, hence
for each hεcs (E). Now if p′≥p, then
and by proposition (1. iv) it follows that
thus E is a space of type (Sλ).
Necessity: Let E be a space of type (Sλ), F be an arbitrary non-archimedean normed space and TεL (E, F). Now for the closed unit ball BF, there exists pεcs (E) such that T (BP (0,1))⊂BF. Since E is a space of type (Sλ), there exists qεcs (E) such that
| |
for all p′≥q. It follows by proposition (1. (iii) ) that
| |
for all p′≥p. Now since,T (BP’ (0,1))⊂T (Bq (0,1))≤ BF)) then (δn(T(Bq (0,1)), BF)) ≤δ (T(Bq (0,1)), T(Bq (0,1)), T (Bp’ (0,1)).
Therefore (δn (T (Bq (0,1)), BF))ελ and so T(Bq (0, 1) is λ-compactoid in F and by proposition (2.i) is λ-limited, Thus T is λ-limited operator.
Definition 7: A locally convex space E over K is called λ-semi-Montel, if every bounded subset D of E is λ-compactoid.
Notes:
| • | Every finite dimensional normed space is λ-semi-Montel. |
| • | If E is λ-Gp space such that every bounded subset of E is λ-limited, then E is λ-semi-Montel space. |
| • | If Eλ-semi-Montel space, then every bounded subset of E is λ-limited. |
Proposition 5:
| • | If E is λ-limited space, then every bounded set in E is λ-limited. |
| • | If F is a locally convex space over K and L (E, F) = λ-lim (E, F) for every non-archimedean normed space E, then every bounded set in F is λ-limited. |
| • | If F is λ-semi-Montel space, then L (E, F) = λ-lim (E, F) for every non-archimedean normed space E. |
| • | If F is λ-Gp space and L (E, F) = λ-lim (E, F) for every non-archimedean normed space E, then F is λ-semi-Montel space. |
Proof:
| • | Let A be any bounded subset of E and let TεL (E, c0 (k)). Since L (E,co (K)) = λ-lim (E, co (K)), then there exists a zero-neighborhood U in E such that T(U) is λ-limited in c0(K). Since A is bounded, then there exists rεK, |r|>0, such that A⊂rU and so T(A)⊂rT(U). It follows by proposition (2.iii) T(A) is λ-limited in c0(K). Since c0(K) is λ-Gp space, then T(A) is λ-compactoid and so A is λ-limited set in E. |
| • | Suppose L (E, F) = λ-lim (E, F) for every non-archimedean normed space E. We shall show that every bounded set A in F is λ-limited. Since A is bounded set in F, then for each pεcs (F) there exists m(p)εK, |m(p)|>0 such that A⊂m(p) Bp (0, 1). Now let, |
Then q is a non-archimedean seminorm on A. If q(y) = 0, then p (y) = 0 for all pεs(F) and so y = 0. Thus q is a non-archimedean norm. Now by E, we shall take the non-archimedean normed space of all yεF with q (y)<∞. If BE = {yεF: q(y)≤1} is the closed unit ball of E, then A⊆BE and if the operator T equal to the identity imbedding of E into F, then TεL (E, F). Since L (E, F) = λ-lim (E, F), then T is λ-limited operator. Thus T (BE) = BE is λ-limited set in F and by proposition (2. iii) A is λ-limited set in F.
| • | Let F be any λ-semi-Montel space, E be a non-archimedean normed space and TεL (E, F). Since T is bounded, then T maps the unit ball BE into E a bounded set T(BE) in F and so T (BE) is λ-compactoid set in F, hence T(BE) is λ-limited set in F. Therefore T is λ-limited operator. |
| • | It follows from part (2) and the fact that the space F is λ-Gp spaces |
Theorem 2: Let F, E be any locally convex spaces over K and let L (E, F) = λ-lim (E, F), then L (E0, F0) = λ-lim (E0, F0) for a complement linear subspace E0 of E and subspace F0 of F.
Proof: Let T0εL (E0, F0) and let TεL (E, F) defined by T(x) = T0 where x = x0+x1, x0εE0. Since L (E, F) = λ-lim (E, F), then T is λ-limited operator and so there exists a zero-neighborhood U in E such that T(U) is λ-limited set. Since U∩E0 is zero-neighborhood in E0, then applying proposition (2.iii) we deduce that T (U∩E0) = T0 (U∩E0) is λ-limited and therefore T0 is λ-limited operator.
Note: If the valuation on K is dense and λ = c0 (K), then L (ι∞ (K), ι∞ (K)) = λ-lim (ι∞ (K), ι∞ (K)) but L (c0 (K), c0(K)) ≠ λ-lim (co (K), co (K)) (De Grande-De Kimpe et al., 1995, Example (2.6.iv)).








