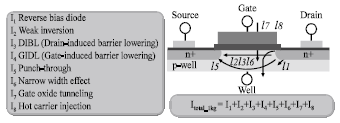
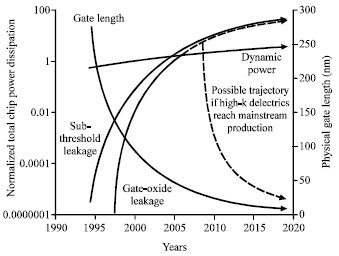
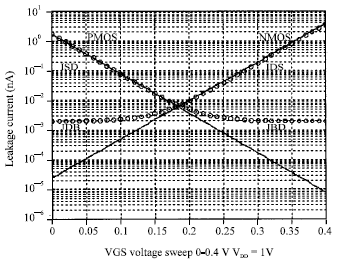
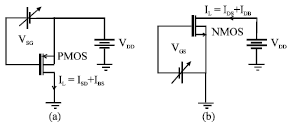
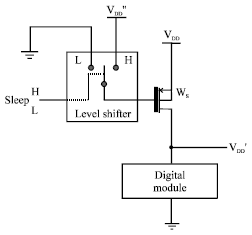
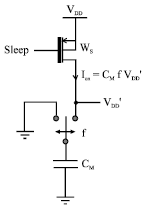
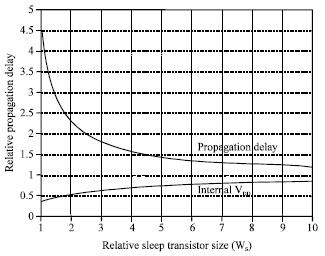
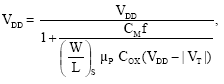Research Article
Sleep Transistor Sizing According to Circuit Speed, Silicon Area and Leakage Current in High-Performance Digital Circuit Modules
Suleyman Demirel University, Electronics and Computer Education, Isparta 32260, Turkey
Steven L. Garverick
Not Available