INTRODUCTION

In a direct transfer reaction, which induced by heavy ions the population of the first few excited levels, is well described by the distorted wave method. For most cases the Distorted Wave Born Approximation (DWBA) is one step process (Mermaz et al., 1983). So, the theory of direct transfer reactions are introduced as a powerful tool (AL-Farra et al., 2003) with which we can obtain information about the structure of nuclei. The differential cross section of ¹²C(³He,n)¹⁴O and ²⁶Mg(³He,n)²⁸Si (AL-Farra et al., 2003) reactions, which leads to the low-lying states in the final nuclei at 45.5 MeV incident energy, have been calculated in terms of DWBA calculations. The two nucleon (Michimasa et al., 2002; Gupta et al., 1976; AL-Farra et al., 2003) and alpha (Shyam et al., 1985) transfer reactions have been studied in term of the DWBA theory. The numerical data of the angular distribution and the experimental data were found in a good agreement especially at forward angles. However, the optical potential plays an important role in calculating the angular distributions and the differential cross section of ¹⁶O(⁶Li,α)¹⁸F (Farra, 2003). And previously studied in term of DWBA using the real and imaginary parts of Wood-Saxon optical potential (WS-WS) and then compared with the Wood-Saxon including the J-dependent (WS-JD). It was found that the inclusion of the J-dependent term gives the same results as the (WS-WS) at forward angles, with a better description at backward regions though.

In the present reserch, the differential cross sections of heavy-ion reactions with α-transfer reactions have been calculated in term of one-step DWBA calculations using different optical potentials (real and imaginary parts are Gobbi and Vandenbosch potential). Where Gobbi and Vandenbosch potentials are members of a family of Woods-Saxon potentials with the same geometrical parameters but different real and imaginary well depths. The calculated differential cross sections are fitted with the experimental data to extract spectroscopic factors.

NUCLEAR OPTICAL POTENTIAL

In this section, the differential cross sections for the Stripping reaction ²⁴Mg (¹⁶O, ¹²C) ²⁸Si and ²⁸Si(¹⁶O, ¹²C)³²S have been evaluated in the framework of one-step DWBA calculations. The calculations used different optical potentials, namely Gobbi potential (Yosio and Taro, 1984), which has the following form

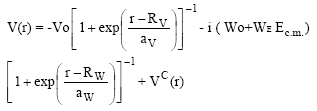(1)

and Vandenbosch potential has the same form as Gobbi potential except

Where, V^C(r) is the Coulomb potential (Jain and Shastry, 1979) due to a uniform sphere of radius R_C and is given by

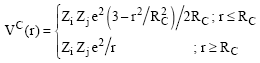(2)

NUMERICAL CALCULATIONS AND RESULTS

To show, how sensitivity the α-transfer differential cross-section to the optical potential, we studied the effect of the optical potentials as follow. The differential cross sections have been numerically carried out for ²⁴Mg(¹⁶O, ¹²C) ²⁸Si reactions at 27.8, 36.2 MeV and ²⁸Si(¹⁶O, ¹²C) ³²S reactions at 26.2 MeV. In the first calculations, the optical potential is assumed to have a real and imaginary Gobbi potential plus Coulomb potential. In the second calculation we used the real and imaginary part is Vandenbosch potential plus Coulomb potential. In both calculations the bound-state wavefunctions between the particles i and j in the initial and final channels are described by a harmonic-oscillator function (Linhua and Guozhu, 1988), which is given by

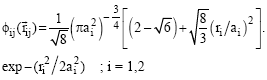(3)

Where α_i is the oscillator length parameter. Throughout this analysis (Table 2), the particle-nucleus interactions are taken to have a double-Gaussian potential (Changun and Pingzhi, 1988)

(4)

Where V_Ri>0 and V_Ai<0 are the strengths of the repulsive and attractive terms respectively, while α_Ri and α_Ai are their decay factors. The realistic finite-range of the reduced form factor is given as

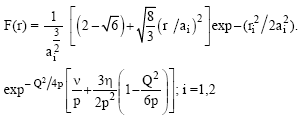(5)

Where

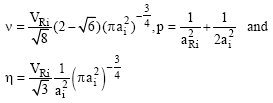Table 1:	Optical potential parameters used in the DWBA calculations

The quantity Q includes the dynamical energies together with both of the nuclear interaction and nucleus-nucleus optical potentials. Therefore, the transition matrix element T_fi for heavy-ion transfer reaction T(A,X)R with a transition particle C is expressed to have the form

(6)

Where, S(l, j) and S*(l', j') are the spectroscopic factors in the initial and final channels, respectively. J_i and μ_i are the respective spin angular momentum of the particle i and its magnetic projection on the z-component. T^ll' is the reduced transition matrix element, which is given by

(7)

Where and are the ingoing and outgoing distorted wave functions, while, φ^l'j' stands for the wavefunction which describes the bound state of the residual nuclei R. However, the differential cross section for heavy ion reaction with particle transfer is described by a clear form, which is given by

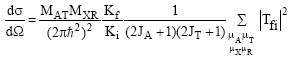(8)

Where K_i and K_f are the wavevectors for the initial and final channels, respectively. Where the bound state wavefunctions for both initial and final channels are expressed to have a harmonic-oscillator wavefunctions, which is given by Eq. (3) with parameters determined to reproduce the particle-particle binding energies. In general, the present spectroscopic factor is extracted from the reaction, that is

(9)

Where N is normalization factor for the reaction

Table 2:	Parameters of gaussian potential

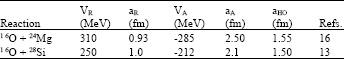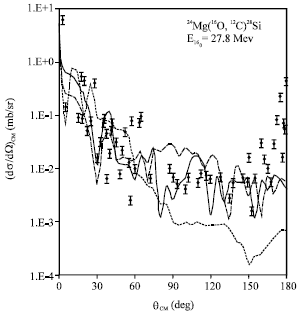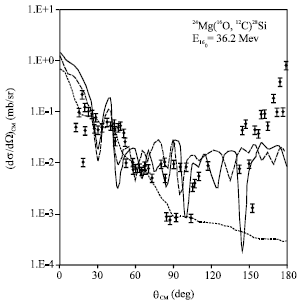
Fig. 1:

The differential cross-section of the 24Mg (16O, 12C) 28Si α-transfer reaction at 27.8 Mev incident energy leading to 0.0 28Si excited state. The solid curve (Vandenbosch potential) and dashed curve (Gobbi potential) are the present calculation. The dotted line is the previous work taken from reference (Kurath, 1973) and the dots are the experimental data taken from reference (Guozhu et al., 1984; Paul et al., 1980)

The parameters of the optical potential are taken as those used in the earlier calculations listed in Table 1. These parameters are found to reproduce the forward angles data reasonably well but they don’t fit the data at large angles. Therefore, the present optical potential obtains the best fit to the data. The results obtained for the differential cross-sections are shown in Fig. 1-3 by the solid and dash lines are compared with previous calculations, shown by the dotted lines and experimental data points.

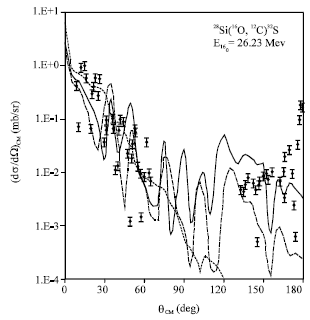
Generally, it is found that the present work is good over the entire angular range as shown in the Fig. 1 and 2, but the predictions are low in magnitude at large angles as seen in Fig. 1 and 2. In Fig. 3, the use of Gobbi potential gives predictions low at large angles, but the use of Vandenbosch potential gives a good result at large angles. Since, the use of Gobbi and Vandenbosch potential leads to a reasonable results better than Woods-Saxon potential at large angles.

Fig. 2:	The differential cross-section of the 24Mg(16O, 12C) 28Si α transfer reaction at 36.2 Mev incident energy leading to 0.0 28Si excited state . The solid curve (Vandenbosch potential) and dashed curve (Gobbi potential) are the present calculation. The dotted line is the previous work taken from (Kurath, 1973) and the dots are the experimental data taken from reference (Sanders et al., 1985)

Fig. 3:	The differential cross-section of the 28Si (16O, 12C) 32S α-transfer reaction at 26.23 Mev incident energy leading to 0.0 32S excited state. The solid curve (Vandenbosch potential) and dashed curve (Gobbi potential) are the present calculation. The dotted line is the previous work taken from reference (Kurath, 1973) and the dots are the experimental data taken from reference (Linhua et al., 1985)

Table 3:	Spectroscopic factors

DISCUSSION

In this study, the differential cross sections of ²⁴Mg(¹⁶O, ¹²C) ²⁸Si and ²⁸Si(¹⁶O, ¹²C) ³²S reactions have been calculated reasonably well using simple one-step DWBA calculations. Then data are analyzed in terms of different optical models. As shown in Fig. 1-3, it is clear that the present optical potential gives a better data fit than the other optical potentials. From Fig. 1, it can be seen that the data of ²⁴Mg(¹⁶O, ¹²C) ²⁸Si at large angles with Gobbi or Vandenbosch potential at 27.8 MeV incident energy is noticeably nearly good and significantly better than the previous work. But when the incident energy is 36.2 MeV, as in Fig. 2, both Gobbi and Vandenbosch potential data deviate away at large angles compared with Fig. 1. This deviation stands more clearly when using Vandenbosch. In Fig. 3, shows the data of ²⁸Si(¹⁶O, ¹²C) ³²S at 26.23 , it is clear that at large angles the use of Gobbi potential was poorer and not significantly different from those shown by the previous research, but the solid line within Vandenbosch potential is better than both Gobbi and the previous work.

CONCLUSION

In conclusion, the present DWBA calculations show satisfactory fit to α-transfer data. Since the calculated cross sections don't change appreciably with the potential type in forward regions. Meanwhile, at the large angles data are extremely sensitive to the potential in use. In addition, the present work the use of either Gobbi or Vandenbosch potential is better than the previous research. The usage of Vandenbosch potential gives better fit than the use of Gobbi potential. Finally, the spectroscopic factor is shown in Table 3.