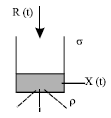
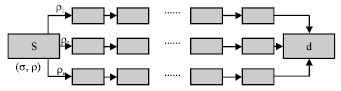
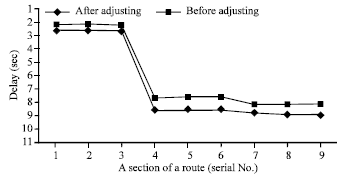
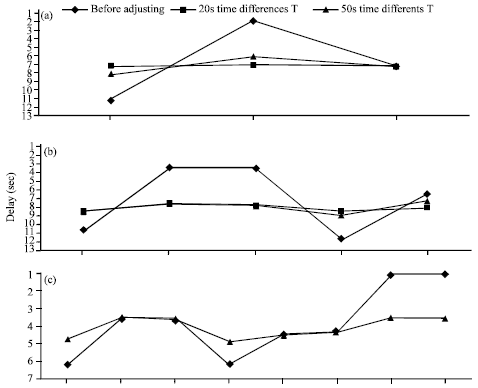
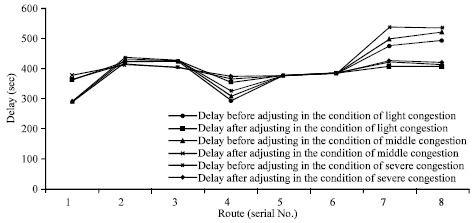
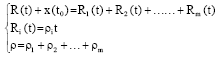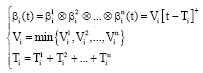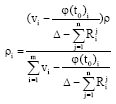Research Article
The Research of Traffic Flow Assignment Model based on the Network Calculus of Computer Network
Jiangxi Normal University, Ziyang Road, Nanchang 330022, China
Wei Fan
Jiangxi Normal University, Ziyang Road, Nanchang 330022, China
Jiayao Liu
Jiangxi Normal University, Ziyang Road, Nanchang 330022, China
Fan Zhang
Jiangxi Normal University, Ziyang Road, Nanchang 330022, China