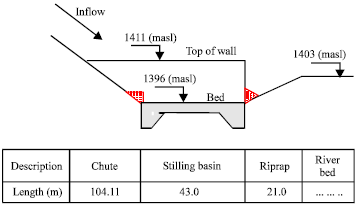
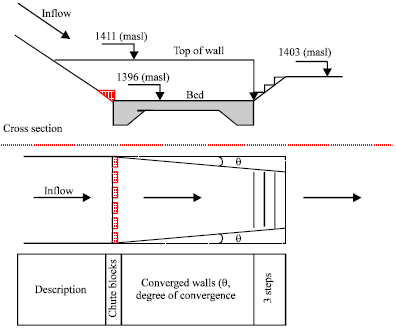
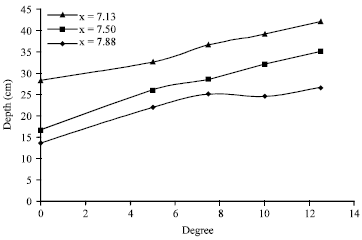
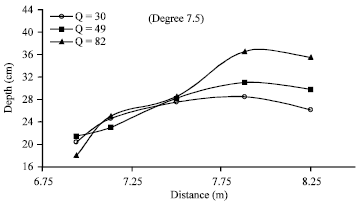
Research Article
Effect of Convergent Walls on Energy Dissipation in Stilling Basin by Physical Modeling
Department of Civil Engineering, Islamic Azad University, South Tehran Branch, Iran
A. Razmkhah
Department of Civil Engineering, Islamic Azad University, South Tehran Branch, Iran
F. Ghobadi
Department of Water Engineering, Islamic Azad University, Science and Research Campus, Iran