Research Article
A Fuzzy Quality Function Deployment Approach to Enterprise Resource Planning Software Selection
Department of Industrial Engineering, Iran University of Science and Technology, Tehran, Iran
Same Yousefi
Member of Young Researchers Club, Islamic Azad University, Central Branch, Tehran, Iran
Mohsen Cheshmberah
Department of Industrial Engineering, Iran University of Science and Technology, Tehran, Iran









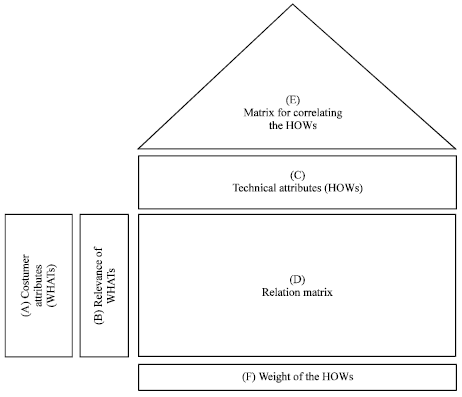
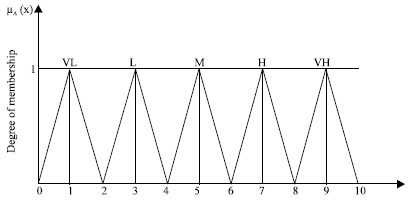




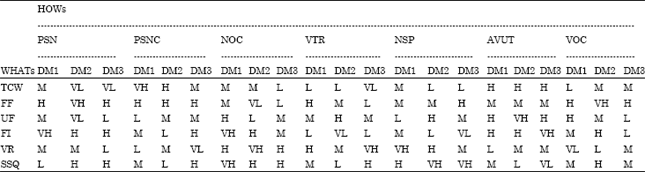
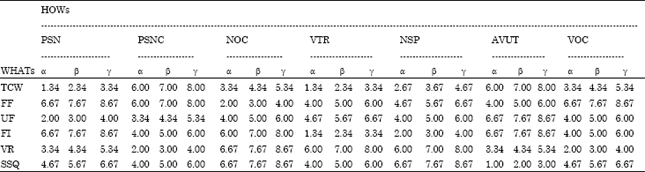
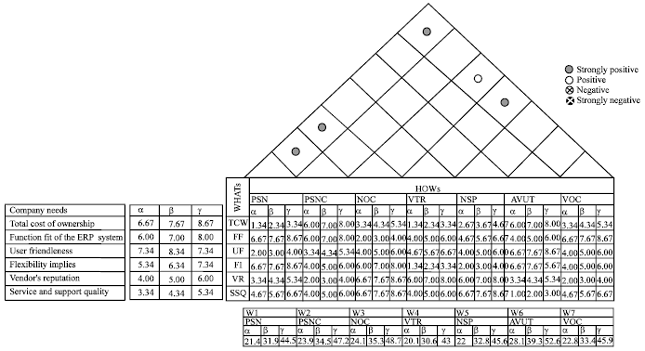

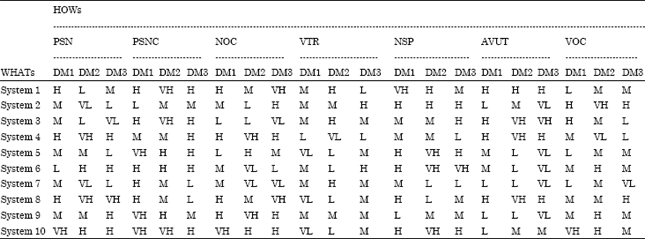
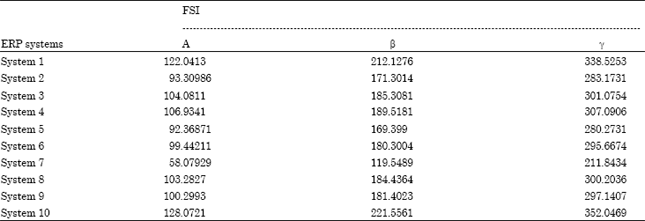

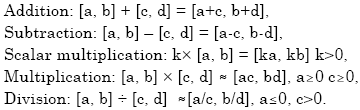 .
.